Rechnen mit Legosteinen – aber richtig!
Immer wieder geistern Unterrichtsideen mit Legosteinen durchs Netz, die als „genial“ und „kreativ“ weiterverbreitet werden. Leider sind sie in der Regel wenig durchdacht. Das gilt zum Beispiel für die Idee einer amerikanischen Lehrerin zum Bruchrechnen mit Lego, die kürzlich von der FAZ aus dem Netz gefischt wurde.
Obwohl (oder weil) ich selbst ein Buch über „Rechnen mit Legosteinen“ geschrieben habe, halte ich Legosteine gerade für das Bruchrechnen für wenig geeignet. Folgendes Beispiel soll angeblich dazu dienen, „den Einstieg in die Rechenwelt so einfach wie möglich zu gestalten“ (FAZ):
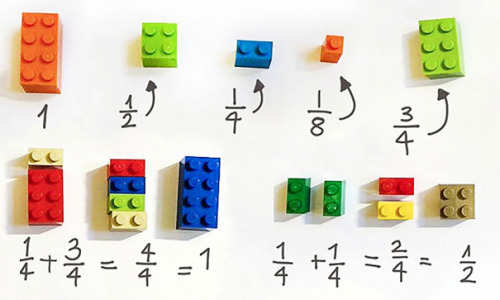
Das kann es aber nicht, denn hier wurde nach der ersten Begeisterung nicht weitergedacht:
Erstens wird, wie so oft, vergessen, dass diese Darstellung nur solchen Schülern hilft, die das Bruchrechnen schon gut verstehen. Schwache Rechner wären verwirrt davon, dass hier eigentlich etwas anderes dargestellt wird, als geschrieben steht, nämlich in Wirklichkeit 8 x ½ = 4, 8 x ¼ = 2 etc. Das wird dargestellt und nicht 1:2 = ½. Freilich sieht das die Urheberin anders, denn sie hat definiert: 1 = ein Achterstein. Genau das ist aber tabu, wenn man wirklich den „Einstieg in die Mathematik möglichst einfach machen will“. Wenn man mit der Definition 1=8 Noppen arbeitet, spricht man damit stark fortgeschrittene Schüler an.
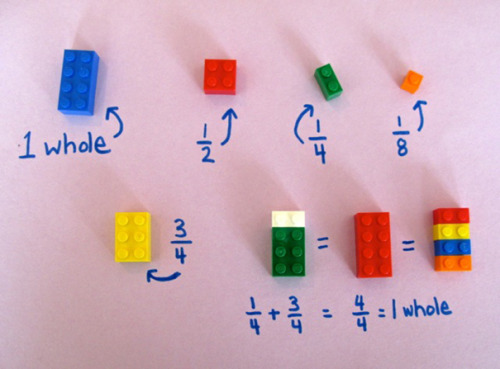
Als Hilfe für schwächere Rechner oder Anfänger funktionieren Legosteine im Rechenunterricht nur gut nach der Regel 1 Noppe = 1. (Dann aber können sie besser sein als alles herkömmliche Material.) Nur in der Darstellung der Quadratzahlen wurde das berücksichtigt, aber auch das ist nicht optimal gelungen:
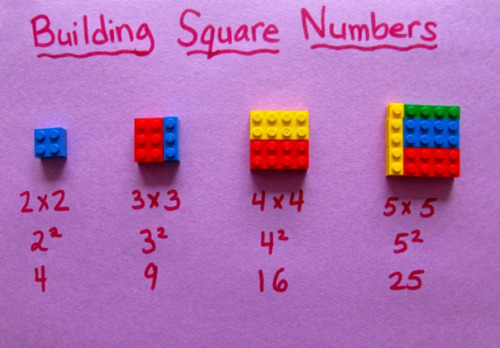
Man sollte für 2 x 2 = 2² zwei Steine der Größe 1×2 Noppen nehmen, für 3 x 3 = 3² drei Dreier-Steine etc. Eindeutigkeit ist wichtig, gerade, wenn man schwachen Rechnern helfen will. Für das Quadrieren sind zwar nur die Längen der Außenkanten entscheidend, aber die Umwandlung in eine Multiplikation, die wiederum eine mehrfache Addition gleich großer Mengen ist, wird nur deutlich, wenn diese gleich großen Teilmengen auch real vorhanden sind. Im Beispiel muss man sich z.B. bei 3 x 3 den roten 6er-Stein als aufgeteilt in zwei Dreier-Steine denken, und das überfordert Schüler, die sich auf die dargestellte Operation konzentrieren sollen. Es wirft bei klugen Schülern die Frage auf, ob das wohl Absicht sei, ob hier ein zusätzlicher Zusammenhang dargestellt werden soll, und kann so zu Missverständnissen führen. Man sollte mit jedem Rechenmaterial nur die Zusammenhänge darstellen, die in der Rechnung vorhanden sind bzw. betont werden sollen, und keine zusätzlichen darstellen, auch nicht versehentlich.
Nocheinmal zurück zum Bruchrechnen: Die abgebildete Idee hat noch einen anderen Pferdefuß.
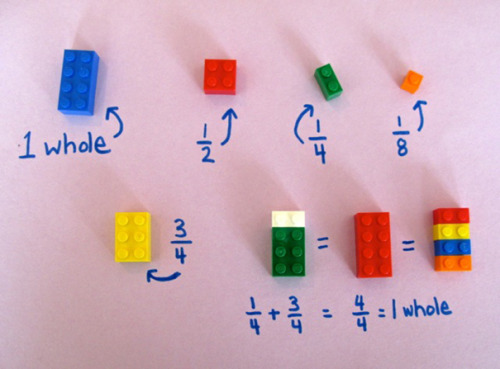
Es sind mit den jeweils gleichen Steinen nur ausgewählte Rechnungen möglich, was dem Konzept des Bruches völlig zuwiderläuft. Wenn man definiert „ein 8er-Stein = 1“, kann man damit z.B. nicht durch 3, 5, 6 etc. teilen. Die 1 kann man aber durch alle Zahlen teilen, das ist ja das Entscheidende am Bruch. Division lässt sich mit Lego gut darstellen, sogar Division mit Rest, aber das Konzept des Bruches nicht – nur Rechnungen mit Brüchen wie 8 x ½ = 4, s.o. Das hilft aber nicht bei der Erarbeitung der Struktur „Bruch“ als allgemeinener Größe.
Da jeder Stein bei der Definition 1 Noppe = 1 bereits einen bestimmten Wert hat, sind Rechnungen wie 1/2 + 5/3 darüber hinaus so schwierig darzustellen, dass dies bestenfalls eine Zusatzaufgabe für besonders fitte Schüler sein könnte, aber keine gute Erarbeitungshilfe für schwache Schüler. (Schaffen Sie’s? Ein Tipp: Versuchen Sie es mit ½ x 6 + 5/3 x 6 anhand von Sechser-Steinen.) Bei Rechnungen wie ½ x 6 + 5/3 x 8 verliert der Einsatz von Material dann endgültig seine Berechtigung – und das macht gar nichts.
Denn Material ist, wie Hans Aebli sagt, nur dort am rechten Platz, wo es die Struktur einer Operation klarer macht. Das eigentliche Lernziel ist nicht, mit Legosteinen Rechnungen darstellen zu können, sondern die Strukturen der Mathematik zu verstehen. Material nimmt einem die Anstrengung nicht ab, die wunderbaren, aber unsichtbaren mathematischen Strukturen zu denken und in der adäquaten, sachlogischen mathematischen Schreibweise wiederzugeben.
Eine überarbeitete, aktualisierte Version von „Rechnen lernen mit Legosteinen“ wird übrigens voraussichtlich im Lauf des Jahres 2016 hier im Blog vorgestellt werden und erhältlich sein! Dort finden Sie fundierte Anwendungen für dieses Material, die wirklich funktionieren und die großen Vorteile der Steine nutzen.

Guten Tag Frau Stiehler,
wird eine Neuausgabe ihres Buches bald kommen? Oder sollte ich auf eine alte gebrauchte Ausgabe zurückgreifen?
Mit freundlichen Grüßen
Tatjana Schütte
Sehr geehrte Frau Schütte,
wie bereits per Email mitgeteilt, ist geplant, im Lauf des nächsten Jahres hier im Blog Videoanleitungen zu vielfältigen Übungen rund um das richtige Rechnen mit Legosteinen zu veröffentlichen. Auch ein neues Ebook dazu ist in Arbeit, es wird aller Voraussicht nach bis spätestens 2018 erhältlich sein. Weiterhin viel Erfolg beim Üben! Herzliche Grüße, Miriam Stiehler
traurig, wenn eltern legosteine brauchen, um ihren kindern etwas beizubringen. (Wegen Obszönität von der Redaktion gekürzt.)
Schwach. Echt schwach den Sinn hinter der Einfachheit beim Bruchrechnen lernen nicht zu erkennen. Schüler müssen im ersten Schritt nicht verstehen, dass die Zahl 1 durch jede beliebige geteilt werden kann, sondern, dass es überhaupt möglich ist. Der einzige Schwachpunkt am Bild der FAZ (und nein ich bin kein Mitarbeiter dort :-)) ist meiner Meinung nach, dass bei 1 nicht 8/8 dabei steht. Aber sie können gerne Versuchen eine endlose Legoplatte herzustellen um den Schülern, am besten in der dritten Klasse, das zu veranschaulichen. Bravo, gute Idee -.- . Sorry über das vernichtende Fazit, Ihre Einschätzung ist nicht falsch, aber schlichtweg zu weit gedacht. Vergleichbar: Jemandem der eine Schreinerlehre beginnt zuerst beibringen zu wollen wie man ein Meisterstück baut bevor man die grundlegenden Dinge lehrt.
Wo ich ihnen zustimmen muss ist, dass das dargestellte System mit den Legosteinen nicht skaliert – das muss es aber auch nicht, denn es schafft ein gutes Grundverständnis.
Hallo B, schwach, dass Sie anonym Ihr „vernichtendes Fazit“ posten. Ihre Einschätzung der didaktischen Notwendigkeiten ist schlichtweg falsch und zu kurz gedacht. Ja, das genannnte Beispiel ist für sich alleine genommen eine ganz nette Erklärung, die ein Elternteil mal eben bei den Hausaufgaben vermutlich ohne größeren Schaden zur Illustration heranziehen kann, wenn das Kind in Mathe generell keinerlei Probleme hat. Besonders könnte man so erklären, was Zähler und Nenner bedeuten (3/4 als „drei von vier Teilen“). Aber selbst in dieser Situation müssen bestimmte Voraussetzungen auf Seiten des Kindes erfüllt sein, sonst richtet man Verwirrung an. Als Konzept für den Unterricht taugt diese Einsatzweise einfach nicht, gerade weil sie, wie Sie selbst schreiben, nicht skaliert. Denn:
– Es ist und bleibt für Schüler unnötig schwierig, dass 1/2 hier gleichzeitig aus 4 Noppen besteht. Das ist als Division korrekt und didaktisch wunderbar einzusetzen: 8:2 = 4. Aber hier werden zugleich unnötigerweise zwei Aspekte eingeführt, obwohl der Aspekt „1/2 bedeutet einer von zwei Teilen“ im Vordergrund stehen sollte. Der zusätzliche Aspekt ist die Mächtigkeit dieses Teils, 1/2 von etwas, das genausogut 2 als auch 2.0000.000 sein könnte. Sobald man noch einen anderen Stein als den 8er ins Spiel brächte, müssten die Schüler verstehen, dass 1/2 im einen Fall nur den Wert 1 hätte und im anderen Fall den Wert eine Million. Zur Einführung in die Brüche wäre das schlicht unnötig verwirrend. Man könnte das mit genau dem einen 8er-Stein punktuell am Übergang von der Division in das Bruchrechnen einsetzen, als einzelne Novelty. Aber als durchgehendes Konzept taugt es eben nicht, sondern schadet sogar, wenn Kinder sich ihre eigenen Gedanken machen und mangels Bruchkenntnissen in die Irre gehen.
– Die Darstellung bildet nur einige ausgewählte Aspekte des Bruches ab, und daher ist sie viel schlechter geeignet als das übliche Pizza-Diagramm. Der Legostein unterschlägt nämlich, dass man 8 durchaus auch in 7 oder 5 Teile teilen kann wenn man möchte. Dass also jede beliebige Zahl im Nenner stehen kann. Nur die Teiler von 8 sind hier mögliche Nenner (daher wurde hier eben auch der 8er gewählt, weil der alternativ verfügbare 6er-Stein nicht in Viertel, eine sehr gängige Teilung, geteilt werden kann). Wenn man das schon machen will, wäre der 12er Stein die bessere Wahl, da er die Teiler 2, 3, 4 und 6 besitzt und somit wenigstens mehr Möglichkeiten zulässt. Wie auch immer: Schüler sollen ein allgemeines Prinzip aus Materialdarstellungen ableiten können. Wenn ein Schüler darauf kommt, dass man durch jede Zahl teilen kann, bringt er das Material hier an das Ende seiner Einsatzfähigkeit. Was sagt denn der Lehrer zu dem Schüler, der einwendet: „Aber man kann doch auch durch 7 teilen, wie stellen Sie das jetzt dar?“ Dann muss der Lehrer sagen: „Ääh, ja, das sollte ja nur ein Beispiel sein, hüstel… ich zeichne dir jetzt mal ein Diagramm, mit dem das geht.“ „Schwach“, denkt der Schüler.
Hallo Frau Stiehler,
Wie ist der aktuelle Stand? Wann wird es die Neuauflage des Buches geben? Ich würde es gern kaufen. Das alte scheint nicht mehr zu haben zu sein.
Vielen Dank und beste Grüße
MU
Hallo MU,
leider lässt es meine Zeit im Moment nicht zu, an der Neuauflage zu arbeiten, und ich kann im Moment nicht sagen, ob es 2018 noch klappen wird. Sorry!
Beste Grüße,
M. Stiehler