„Achte auf das Rechenzeichen!“ Wirklich? – Der Klappfehler

Wie kommen Kinder auf Rechnungen wie 14 + 5 = 11? Warum irrt sich die Lehrkraft, wenn sie denkt, das Kind hätte lediglich das Rechenzeichen missachtet? Und warum verursacht eine bestimmte Lehrmethode diesen Fehler?

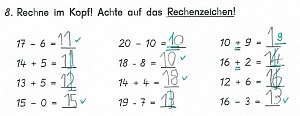
Hier ein Beispiel aus einer Klassenarbeit:

Das sind die Rechnungen des Kindes. Darunter schreibt die Lehrkraft:

Man versteht, dass die Lehrkraft anmerkt, das Kind habe vor allem das Rechenzeichen nicht beachtet. Schließlich war es in der Aufforderung extra unterstrichen, und im Sinne einer Verhaltensinterpretation anstelle einer nüchternen Beobachtung wird hier Unaufmerksamkeit unterstellt, schließlich gehen die Rechnungen ja tatsächlich „in die falsche Richtung“. Aber es genügt leider nicht, bei dieser Einschätzung stehen zu bleiben. Man unterliegt sonst einer unbewussten Verzerrung, einem typischen Beobachterfehler, anstatt dem Problem auf den Grund zu gehen. Um das Problem gründlich zu erfassen, sollte man die Fehler analysieren und gruppieren. Dabei zeigt sich, dass nur bei zweien von ihnen primär die Nichtbeachtung des Rechenzeichens das Problem war:

Bei 10 + 9 = 1 wurde gerechnet 10 – 9 = 1.

Bei 16 + 2 = 14 wurde gerechnet 16 – 2 = 14.

Bei den übrigen Aufgaben ist das Rechenzeichen zwar involviert. Aber dass es nicht beachtet wurde, ist das kleinere Problem. Das Kind ist offenbar in der Lage, zu addieren und zu subtrahieren, die Rechenzeichen werden grundsätzlich verstanden.  

Die anderen Fehler kommen nicht einfach zustande, indem das Kind das gegenteilige Rechenzeichen verwendet:

14 + 5 = 11 entsteht nicht durch die irrtümliche Berechnung von 14 – 5 (= 9)

13 + 5 = 12 entsteht nicht durch die irrtümliche Berechnung von 13 – 5 (= 8)

20 – 10 = 0 entsteht nicht durch die irrtümliche Berechnung von 20 + 10 (= 30)

19 – 7 = 13 entsteht nicht durch die irrtümliche Berechnung von 19 + 7 (= 26)

12 + 6 = 16 entsteht nicht durch die irrtümliche Berechnung von 12 – 6 (= 6)

Eine der Aufgaben fällt aus der Gruppe heraus, nämlich 19 – 7 =  13; hier wurde sicherlich gezählt und/oder die Aufteilung der 9 wird nicht beherrscht, daher der Fehler um 1. (Das Kind zählt sieben Schritte weit: „9, 8, 7, 6, 5, 4, 3“ und schreibt die 3 hin.)

Die anderen Aufgaben gehen alle auf den sogenannten „Klappfehler“ zurück. Was ist ein Klappfehler?

„Unter dem „Klappfehler“ versteht man die Umdrehung der Rechenrichtung auf dem Stellenwert einer Minus-Rechnung, auf dem eine Stellenunterschreitung nötig wäre.“ (Zitat aus Kopf und Zahl Heft 13, S. 10) Wie man oben sieht, findet das gleiche Vorgehen aber auch bei Plus-Rechnungen Anwendung.

Bei Minus-Rechnungen wäre der typische Klappfehler: 13 – 7 = 14  (oder evt. 4). Das Kind denkt dabei: „13 – 7, kann ich nicht. Aber 7 – 3 geht, das ist 4. Also schreibe ich die 1 wieder hin und die 4 dahinter.“ Beim obigen Beispiel hat das Kind wie folgt gedacht: „14 + 5 = 11, weil 5 – 4 = 1, und die andere 1 schreibe ich einfach wieder hin, also 11.“ Wie kommen Kinder auf so etwas?

Zum einen weisen diese Fehler darauf hin, dass mit der verwendeten Lehrmethode die Mächtigkeit der Zahlen über 10, die Handhabung und Bedeutung des Zehners nicht erfolgreich vermittelt wird. Der Klappfehler ist ein ganz typisches Beispiel für sog. didaktogene, also durch Unterricht erzeugte oder zumindest deutlich verstärkte Fehlstrategien im Rechnen. Er zeigt, dass den Schülern noch nicht verständlich gemacht wurde, wie das Dezimalsystem wirklich funktioniert und wie man mit dem Zehner umgeht. Der Klappfehler ist der Versuch der Schüler, durch einen eigenen Algorithmus oder „Rechentrick“ ein Ergebnis abzuliefern, mit den Mitteln, die ihnen vor dem Hintergrund des fehlenden Verständnisses zur Verfügung stehen.

Zum anderen wird der Klappfehler angebahnt durch die gut gemeinte, aber schädliche Verwendung des Rechentricks „Die kleine Aufgabe hilft“ oder „Rechne einfach mit der Einerstelle“. Dabei lernen die Kinder, den „Zehner“ einfach wegzulassen und nur mit den Einern zu rechnen. Zu diesem Zeitpunkt kennen sie meist noch keine Zahlen größer als 20, und daher wird der Zehner gar nicht als Bündel von 10er-Gruppen aufgefasst, sondern letztlich nur als eine Ziffer „1“, die man vornehinschreiben oder eben auch weglassen kann oder muss, je nach Situation. Die vermeintlich hilfreiche Taktik mit der „kleinen Aufgabe“ geht auch im vorliegenden Fall dem Klappfehler voran. In der gezeigten Klassenarbeit wird genau diese Strategie in der vorhergehenden Aufgabe verlangt und das betreffende Kind wendet sie wie von der Lehrkraft gewünscht an:

Was bewirkt das beim Schüler? A. von Schwerin erklärt es am Beispiel der falschen Rechnung 15 – 7 = 12: „Durch die Abtrennung des Zehners entsteht beim Zehnerübergang der Subtraktion für unseren Erstklässler auch noch ein anderes Problem: Was tun, wenn zu rechnen ist 15 – 7? Nach dem routinierten Wegdenken der Zehn müsste man ja nun 5 – 7 rechnen. Manche Schüler lesen die Rechnung sogleich als 7 – 5, so kennt man sie schließlich. Andere erinnern sich an das Gebot, immer nur von der größeren die kleinere Zahl abzuziehen. Aber: „Irgendetwas“ muss ja gerechnet werden, also dreht man die Rechnung bewusst um zu: 7 – 5 unter dem Motto: „Was nicht passt, wird passend gemacht.“ Oder der Schüler ergänzt: 5 + wie viel ist 7. Die ergänzte 2 wird festgehalten. In allen Fällen ergibt sich auf der Einerstelle 2, die „weggelegte“ Zehn wieder dazu, erhält man als Ergebnis 12. Das stimmt dann nicht. Aber so wird der Klappfehler „geboren“.“

Das eigentliche Problem in der obigen Klassenarbeit ist also nicht, dass das Kind die Rechenzeichen nicht beachtet. Es liegt viel, viel tiefer und seine Lösung würde von der Lehrkraft eine grundlegende Änderung in ihrem Unterricht verlangen. Eine ganze Menge ihrer Kopiervorlagen wären ab sofort unbrauchbar und sie müsste zukünftig den Aufbau des Zehnerübergangs anders gestalten, u.a. wie bei Gaidoschik an diversen Stellen beschrieben. Man sollte von vornherein nicht erst wochenlang Zahlen bis 10, dann wochenlang Zahlen bis 20 besprechen, sondern mit Überschreitung des 10ers den ganzen Zahlenraum bis 100 bearbeiten. Nur so wird der Charakter des Dezimalsystems deutlich. Das ist viel Arbeit. Doch mit der Methode „Die Kleine Aufgabe hilft“ werden die tatsächlichen mathematischen Zusammenhänge leider verschleiert und die Kinder verführt, ohne Verstand ein oberflächliches Vorgehen nachzuahmen.

Der eigentliche Knackpunkt ist also, wie so häufig, die Didaktik. Im oben verlinkten Artikel wird sehr ausführlich beschrieben, welche weiteren Probleme die vermeintliche Hilfestellung der „Kleinen Aufgabe“ birgt und wie man sie umgehen könnte.

Dieses Beispiel zeigt aber auch, warum besserer Unterricht nicht nebenbei entsteht. Besserer Unterricht ist viel Aufwand: Man muss den Aufbau mehrerer Wochen neu strukturieren, passende Erklärungen und Handlungsformen überlegen, sinnvolles Material beschaffen (während man vielleicht gerade erst Muggelsteine o.ä. gekauft hat), neue Arbeitsblätter erstellen (wobei tatsächlich ein Heft- und-Tafel-basierter Unterricht in vieler Hinsicht die effizientere Lösung wäre), vielleicht sogar vom vorhandenen Buch abweichen und idealerweise die Eltern instruieren oder zumindest informieren, damit sie die richtige Herangehensweise zu Hause übernehmen. Das ist eine Menge Arbeit. Sie ist notwendig und wichtig, aber wenn man die oder der einzige im Kollegium ist, die sie sich macht, hält schnell das Gefühl Einzug „Ich bin hier die Dumme, die es sich schwer macht.“. Umso wichtiger wäre es, dass Schulleitungen oder Fachbereichsleiter sich wirklich für didaktische Fragen zuständig fühlen und sich entsprechend engagieren, z.B. in hilfreichen (!) Unterrichtsbesuchen und Tipps oder durch Fachteams, in denen gemeinsam der neue Aufbau durchdacht und Aufwand geteilt wird. Denn, so dankbar man für die Fehleranalyse-Kompetenz mathematischer Institute sein muss: Ein guter Zustand ist es nicht, wenn deren Wissensstand den mancher  Lehrkräfte übertrifft und wenn dieses Wissen als besonderes Extra, nicht als wesentlicher Teil der Didaktik wahrgenommen wird.